Die meisten Texte dieser Homepage sind Ausschnitte aus den beiden Büchern Die Struktur der Wirklichkeit und Der Begriff der Wirklichkeit.

Ist die Welt nichtlokal? Druckversion

96 Prozent dessen, was das Universum enthält, sind zurzeit völlig unbekannt. Für 22 Prozent – die sogenannte dunkle Materie – gibt es einige Kandidaten in verschiedenen spekulativen Konzepten jenseits des Standard­modells der Teilchenphysik, was aber die restlichen 74 Prozent – die sogenannte dunkle Energie – betrifft, sind wir vollständig ahnungslos.

Vielleicht ist also jetzt, angesichts einer solch ungeheuren terra incognita, ein geeigneter Zeitpunkt, erneut die allgemeinste und grundlegendste aller Fragen zu stellen:

Woraus besteht die Welt?

Gegenwärtig kann diese Frage nur mit einem klaren: "Wir wissen es nicht!" beantwortet werden. Das allein wäre schon beunruhigend, aber unsere Lage ist tatsächlich noch viel schlimmer, ja geradezu hoffnungslos: Wir scheinen sogar zugeben zu müssen, dass wir gar nicht wissen können, woraus die Welt letztlich besteht und was auf dem Grund der Dinge vor sich geht. Para­digmatische Szenarien aus der Quanten­mechanik – etwa das "Doppelspalt­experiment" – demonstrieren die Aussichts­losigkeit jedes Versuchs, sich einen Begriff davon zu machen, was dort wirklich geschieht.

Ist dieses Scheitern endgültig? Sind unsere Begriffe für das Verständnis der Wirklichkeit tatsächlich so vollständig ungeeignet?

Die Antwort ist nein!

Im Rahmen dieser kurzen Einleitung ist es allerdings nicht möglich, zu beschreiben, wie das Verständnis der Wirklichkeit wieder­hergestellt werden kann. Aber ich werde zumindest einen Anfang machen, indem ich skizziere, wie der scheinbar unwider­legbare Beweis der quanten­mechanischen Nichtlokalität – die sogenannte Bellsche Ungleichung – durch einen einfachen Wechsel der Sichtweise außer Kraft gesetzt wird.

In der historischen Entwicklung der Interpretation der Quanten­theorie war es dieser Beweis, der allen Versuchen ein Ende setzte, eine konkrete Vorstellung davon zu gewinnen, was Quantenobjekte eigentlich sind und was sich bei quanten­mechanischen Mess­prozessen tatsächlich ereignet. Falls man diese ontologische Blindheit nicht akzeptiert, sondern nach wie vor anstrebt, die Wirk­lich­keit zu begreifen, dann muss der erste Schritt also die Wider­legung ebendieses Beweises sein.

Was ist "Nichtlokalität"? Das lässt sich anhand des Einstein-Podolsky-Rosen-Paradoxons erklären. Zu dessen Verständnis reichen einige wenige Fakten:

(1)Durch die quanten­mechanische Beschreibung eines Objekts wird für einige Attribute kein eindeutiger Wert festgelegt, sondern nur die Wahrschein­lichkeits­verteilung möglicher Messwerte.

(2)Das gilt auch im Fall zweier räumlich getrennter Objekte, die in der Vergangenheit miteinander in Wechsel­wirkung standen oder die dem Zerfall eines Objektes entstammen.

(3)Zwischen den Ergebnissen bestimmter Messungen an diesen beiden Objekten besteht dann ein Zusammen­hang, der "Verschränkung" genannt wird. Z.B. sind bei zwei identischen Teilchen A und B, die aus dem Zerfall eines ruhenden Objektes hervorgegangen sind und sich vom Ort des Zerfalls in entgegen­gesetzte Richtungen entfernen, die Impulse in derselben Weise miteinander verknüpft wie in der klassischen Physik, d.h. mit Ausnahme des Vorzeichens sind sie identisch. Ein anderes Beispiel: Zerfällt ein Spin-0-System in zwei Photonen, dann sind die gemessenen Polarisations­richtungen der beiden Photonen zueinander rechtwinkelig.

Das ist schon alles! Was ist daran paradox? Auch das ist schnell erklärt:

Nehmen wir an, es wurde noch keine Messung durchgeführt. Dann ist also bloß die Wahrschein­lichkeits­verteilung der möglichen Messwerte bekannt. Wird aber jetzt der Impuls von Teilchen A gemessen, dann ist wegen (3) natürlich auch im selben Augenblick der Impuls von Teilchen B gegeben, und ebenso verhält es sich im Fall der Photonen­polarisation.

Man kann nun mit Einstein, Podolsky und Rosen folgender­maßen argumentieren:

B ist von A beliebig weit entfernt. Die Messung des Impulses von A kann daher keinen Einfluss auf B haben. Wenn also nach der Messung des Impulses von A auch der von B gegeben ist, dann muss das Ergebnis der Messung von B schon vor der Messung von A festgestanden haben – andernfalls hätte ja die Messung von A eine Zustands­änderung von B bewirkt. Da aber die quanten­mechanische Beschreibung diesen Impuls nicht enthält, ist sie unvoll­ständig. (Der Impuls wäre in diesem Fall ein sogenannter verborgener Parameter.)

Ein plausibles Argument! Die Alternative wäre ja, einen nichtlokalen Zusammenhang zwischen den beiden Messwerten anzunehmen, d.h. einen Zusammenhang, der entweder eine überlicht­schnelle Übermittlung erfordert oder überhaupt ohne einen vermittelnden Prozess existiert und einfach als solcher hingenommen werden muss.

Wie John Bell fast 30 Jahre später zeigte (John Stewart Bell, On the Einstein Podolsky Rosen Paradox, Physics, 1, 195-200, 1964), hat aber diese scheinbar so vernünftige EPR-Annahme – dass das Mess­ergebnis an B schon vor der Messung an A feststeht, weil es einfach einer Eigenschaft von B entspricht – eine Konsequenz, mit der Einstein, Podolsky und Rosen nicht gerechnet hatten.

Bell bewies Folgendes:

Unter der Voraussetzung, dass die EPR-Annahme richtig ist, gibt es Experimente, bei denen die Messresultate signifikant von den Voraussagen der Quantenmechanik abweichen. Solche Experimente wurden durchgeführt. Die Entscheidung war eindeutig: Die Voraussagen der Quantenmechanik wurden bestätigt, die EPR-Annahme wurde somit widerlegt. Das bedeutet: Vor der Messung an A hat B keinen eindeutigen Impuls, danach aber schon. Die Messung an A hat tatsächlich eine Änderung des Zustands von B bewirkt!

EPR hatten beabsichtigt, für eine lokale Wirklichkeit zu argumentieren, d.h. für eine Wirklichkeit, in der ein Objekt auf ein anderes, räumlich distanziertes Objekt nicht anders einwirken kann als durch einen physikalischen Prozess. Durch Bells Intervention scheint aber nun bewiesen, dass es außerdem noch Zusammenhänge ganz anderer Art gibt: solche nämlich, die entweder mit Über­lichtgeschwindigkeit vermittelt werden oder sogar ohne jede Vermittlung existieren. Einstein bezeichnete sie als "spukhafte Fernwirkungen".

John Bell hat seinen Beweis so allgemein wie möglich formuliert. In dieser verallgemeinerten Form des Beweises ist es nicht notwendig, dass es "Objekteigenschaften" sind, die das Messergebnis im voraus spezifizieren, sondern es können beliebige Parameter sein. In seinen Worten: "Let this more complete specification be effected by means of parameters λ. It is a matter of indifference in the following whether λ denotes a single variable or a set, or even a set of functions, and whether the variables are discrete or continuous." (John Bell, a.a.O. p. 196).

Durch diese Verallgemeinerung wird der Geltungsbereich des Beweises erweitert. Da überdies in den Beweis außer der Annahme der Parameter λ (und natürlich Logik und Mathematik) keine weiteren Voraussetzungen eingehen, scheint sich sogar zwingend Folgendes zu ergeben:

Jede Wirklichkeit, die den Gesetzen der Quantenmechanik gehorcht, ist nichtlokal.

Soweit also die Sachlage. In der Physik gilt die Frage der Lokalität bzw. Nichtlokalität damit als erledigt, und Verschränkung ist ein vielbeachtetes, aktives Forschungsgebiet.

Für uns soll jedoch die Darstellung der üblichen Sichtweise bloß als Vorbereitung dafür dienen, dass wir uns unserer eigentlichen Aufgabe zuwenden können, der Antwort auf die Frage:

Warum gilt der Bellsche Beweis in unserer Wirklichkeit nicht?

Um das zu zeigen, werde ich auf die Modell­vorstellung zurückgreifen, die ich bei der Analyse des Doppelspalt­experiments entwickelt habe; Sie ermöglicht eine realistische und lokale Interpretation des Experiments, die sich auf das EPR-Szenario übertragen lässt. Ich werde also kurz skizzieren, was sich gemäß meiner Interpretation bei diesem Experiment wirklich ereignet. (Die folgende Darstellung ist allerdings extrem verkürzt. Für ein besseres Verständnis empfiehlt es sich, hier oder auch hier nachzu­lesen.)

Zunächst löst sich ein Elektron aus einem Orbital (einer Elektronenhülle). Hier die Bilder einiger Orbitale:

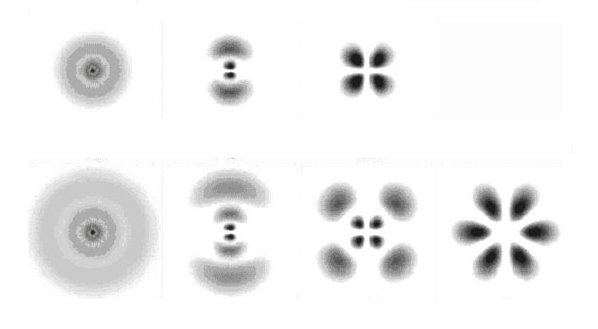"Elektronenhüllen" entsprechen also Schwingungszuständen einer Kugel, mit anderen Worten: sie SIND dreidimensionale stehende Wellen. Wenn sich ein "Elektron" aus einer solchen stehenden Welle löst, dann wird (sozusagen) ein Teil der stehenden Welle zu einer laufenden Welle. Die verbleibende stehende Welle hat dann eine Knotenfläche weniger. Das Elektron – die laufende Elektronenwelle – durchquert danach den Doppelspalt. Nach dem Doppelspalt läuft sie auseinander und interferiert mit sich selbst. Schließlich trifft sie auf die Detektorplatte, d.h. sie trifft überall dort, wo ihre Amplitude nicht Null ist, wiederum auf ein Orbital – auf eine stehende Elektronenwelle. Da etliche dieser stehenden Wellen nahe an der Grenze sind, über der sie in den nächsthöheren Zustand "springen" – den Zustand mit einer Knotenfläche mehr – löst die laufende Welle mit einer gewissen Wahr­scheinlichkeit irgendwo einen solchen Sprung aus, und das bedeutet: an dieser Stelle erscheint ein "Elektron".

Der Rest der laufenden Elektronenwelle verschwindet nicht wie bei der Standardinterpretation, sondern addiert sich zu den anderen stehenden Elektronenwellen, wodurch überall die Wahr­scheinlichkeit zunimmt, dass die nächste laufende Elektronenwelle oder irgendeine später folgende einen Sprung verursacht.

Um nun den Zusammenhang mit dem EPR-Szenario herzustellen, betrachten wir das "Objekt", das wir soeben beschrieben haben, also das "Elektron".

Fragen wir uns zunächst: Hat dieses Elektron einen Ort?

Dem Elektron, das schließlich auf der Detektorplatte beobachtet wird, können wir zweifellos einen relativ genau definierten Ort zuschreiben. Aber wie wir ja wissen, ist dieses Elektron nicht das Elektron, das vorher unterwegs war. Der neu entstandene Schwingungsbereich in der stehenden Elektronen­welle, der in unserer Sicht das beobachtete Elektron ist, enthält nur einen winzigen Bruchteil der ganzen laufenden Welle, die das Elektron vorher war. Der Rest der laufenden Welle ist nun auf alle anderen stehenden Wellen verteilt.

Wir stellen also fest: Das Elektron, das wir beobachten, hatte vor der Beobachtung keinen definierten Ort, weil es dieses "Elektron" vorher überhaupt nicht gab!

Es ist zu sehen, dass die Modellvorstellung, die dem Argument von Einstein, Podolsky und Rosen zugrunde liegt, vollkommen ungeeignet ist. Sie dachten an ein Objekt, das stets mit sich identisch bleibt und sich auf einer Bahn bewegt, so dass es zu jedem Zeitpunkt einen eindeutig definierten Ort hat. Damit ist klar, dass die EPR-Annahme, das Objekt-Attribut existiere bereits vor der Messung, falsch ist.

Wie steht es mit der oben erwähnten Verallgemeinerung in Bells Beweis, bei der es nicht das Objekt-Attribut ist, das den Messwert festlegt, sondern beliebige Parameter λ?

Diese Frage führt uns nun direkt zum Kern unserer Widerlegung des Bellschen Beweises. Folgendermaßen:

Wie aus dem obigen Zitat hervorgeht, setzt Bell die Existenz von Parametern λ voraus, die bei beliebigen Messungen an den gewählten Objekten für die "genauere Festlegung" (more complete specification) der Messwerte sorgen. ("Genauer" deshalb, weil sie ja in der Quantenmechanik nicht existieren bzw. "unscharf" sind). Die Existenz der Parameter λ stellt sicher, dass wir in jedem Fall voraussagen können, was das Messergebnis sein wird.

Im Zentrum des Bellschen Beweises steht eine Ungleichung, die sowohl Resultate von Messungen enthält, die tatsächlich durchgeführt werden können, als auch Resultate weiterer, hypothetischer Messungen an denselben Objekten. ("Hypothetisch" deshalb, weil die Messobjekte natürlich kein weiteres Mal zur Verfügung stehen.)

Das bedeutet:

Das Wissen, zu welchen Resultaten weitere Messungen an denselben Objekten führen würden, ist für die Aufstellung des Beweises notwendig. Ohne dieses Wissen gibt es keinen Bellschen Beweis.

Kehren wir nun wieder zu unserer Modellvorstellung zurück. Ist es hier möglich, die Ergebnisse weiterer Messungen an denselben Objekten vorauszusagen?

Nehmen wir an, wir haben ein Elektron erzeugt. Es durchquert den Doppelspalt, läuft auseinander und interferiert mit sich selbst. Ein winziger Teil des Elektrons regt eine stehende Elektronenwelle auf der Oberfläche der Detektorplatte zum Sprung in den nächsthöheren Zustand an. An dieser Stelle zeigt sich ein schwarzer Punkt. Ein Elektron ist erschienen. Wir haben den Ort dieses Elektrons gemessen.

Können wir nun mit dem Elektron, das wir zuvor erzeugt haben (es ist nicht dasjenige, dessen Ort wir soeben gemessen haben!), eine weitere Messung durchführen? Natürlich nicht – dieses "Elektron" existiert ja nicht mehr bzw. ist jetzt auf alle Orbitale verteilt –, aber wir können ein Elektron erzeugen, das mit dem zuvor erzeugten annähernd identisch ist, und das ist im Rahmen unseres Gedankengangs ausreichend: Wir führen zwar keine weitere Messung an demselben Objekt durch, aber wir wiederholen den Messprozess.

Jetzt zur entscheidenden Frage: Was wird geschehen, wenn dieses Elektron die Detektorplatte erreicht? An welchem Ort auf der Detektorplatte wird ein Elektron auftreten?

Die Antwort ist: Wir können es nicht wissen. Der Ort des nächsten Sprungs – d.h. des nächsten Erscheinens eines Elektrons – hängt eben nicht nur von der Amplitudenverteilung der Welle ab, die auf die Platte trifft, sondern auch davon, wie weit die stehenden Elektronenwellen auf der Platte jeweils von der Grenze entfernt sind, über der sie in den nächsten Zustand springen, und das ändert sich fortwährend. Es gibt keinen Messprozess, in dem bei allen Elektronenwellen die Abstände von dieser Sprunggrenze gleich denjenigen Abständen sind, die sie in irgendeinem anderen Messprozess haben. ("Abstand" ist hier dadurch definiert, wie groß das Amplitudenquadrat der auftreffenden Elektronenwelle mindestens sein muss, um einen Sprung in den nächsthöheren Zustand auszulösen).

Mit anderen Worten:

Es ist unmöglich, den Ort des Erscheinens irgendeines Elektrons vorauszusagen.

Was wir soeben für eine Ortsmessung beim Doppelspaltversuch gezeigt haben, das gilt ebenso für die Messungen der Attribute verschränkter Objekte in EPR-Szenarien. Betrachten wir etwa den experimentell am besten untersuchten Fall: Polarisationsmessungen an verschränkten Photonen.

Zuerst die übliche Beschreibung: Photonen werden paarweise erzeugt. Auf ihren Wegen erreichen sie Polarisatoren, die sie mit einer gewissen Wahrscheinlichkeit durchqueren. Falls sie durchkommen, treffen sie auf einen Detektor und ein Photon wird registriert. Falls sie nicht durchkommen, erscheint kein Photon.

Jetzt die Erklärung, was wirklich geschieht. Sie folgt demselben Prinzip wie beim Doppelspalt-Szenario: Photonen SIND Lichtwellen. Beim Durchgang durch die Polarisatoren verringern sich ihre Amplituden um den Faktor cos α (α ist der Winkel zwischen der Schwingungsrichtung der Welle und der Ebene des Polarisators). Wenn eine Lichtwelle den Detektor erreicht, dann verursacht sie vielleicht den Übergang einer stehenden Elektronenwelle in einen höheren Zustand – dann wird ein "Photon" detektiert. Falls kein Übergang stattfindet, dann addiert sich die Lichtwelle dennoch zu einer oder mehreren Elektronenwellen und erhöht dadurch die Wahr­scheinlichkeit eines Übergangs beim Auftreffen der nächsten Lichtwelle oder einer später folgenden. Das heißt: jede spätere Messung wird von jeder früheren beeinflusst. Selbst wenn es uns also gelingen würde, dieselben Photonenpaare nochmals zu messen, wäre es nicht möglich, die Messresultate vorauszusagen.

Bells Beweis wäre nur dann durchführbar, wenn die Versuchsserien aus Messungen bestünden, die voneinander unabhängig sind. Es müsste also Folgendes gelten: sobald ein Messresultat vorliegt, ist der betreffende Messprozess vollkommen abgeschlossen und wirkt sich nicht auf die weiteren Messprozesse aus. (Bei einer Änderung der Reihenfolge würden die jeweiligen Messresultate unverändert bleiben.)

In unserem Modell ist das offenbar nicht der Fall: Wie soeben erläutert, verändert jede laufende Lichtwelle, die auf den Detektor trifft, einige der stehenden Elektronenwellen (Orbitale) – auch dann, wenn diese Änderung zu keinem Sprung in den nächsthöheren Zustand führt. Es gibt hier also keine Versuchsserien, die aus voneinander unabhängigen Einzeler­eignissen bestehen, sondern nur Versuchsserien, bei denen jede spätere Messung von jeder früheren beeinflusst wird. Somit ändern sich die Ausgangs­bedingungen der einzelnen Messungen auf unvorhersehbare Weise, sodass die Resultate der Messungen nicht vorausgesagt werden können, und das bedeutet:

Es existieren keine Parameter λ, aus denen die Messresultate folgen. Der Bellsche Beweis kann nicht abgeleitet werden.

Um hier keine Unklarheit aufkommen zu lassen, möchte ich noch einmal auf den wesentlichen Punkt hinweisen. Natürlich gibt es in meinem Modell Parameter, durch die jedes Messresultat vollständig determiniert ist, aber da zu diesen Parametern jedenfalls auch zählt, wie weit die stehenden Elektronenwellen beim Auftreffen der Lichtwelle von der Grenze zum Sprung in den nächsthöheren Zustand entfernt sind, genügen diese Parameter nicht der Bedingung, die für Bells Parameter λ erfüllt sein muss: Bells Parameter machen die Messung an einem bestimmten Objekt wiederholbar, sie sorgen dafür, dass die Resultate weiterer Messungen an demselben Objekt bekannt sind. Die "Abstände" von der Sprunggrenze sind jedoch bei jeder neu durchgeführten Messung verändert (vermutlich sind sie auch unabhängig von jeder Messung ständigen Schwankungen unterworfen), und damit ändert sich auch das Resultat der Messung an einem bestimmten Objekt bei jeder Wiederholung. Somit gibt es keine genauere Voraussage irgendeiner Messung – es bleibt bei der quanten­mechanischen Wahrscheinlichkeit.

Damit haben wir unser Ziel erreicht. Dafür war es nicht einmal erforderlich, auf den Beweis selbst einzugehen – die Analyse des Messprozesses war für unsere Argumentation vollkommen ausreichend.

Was hier allerdings fehlt, ist eine detaillierte Beschreibung dessen, was sich bei EPR-Versuchs­serien wirklich ereignet. Wenn der Messwert vor der Messung nicht vorausgesagt werden kann – was sorgt dann eigentlich für den Zusammenhang der Messwerte der verschränkten Objekte?

Im Begriff der Wirklichkeit habe ich zwei Formeln für die Ereigniswahrscheinlichkeiten angegeben, die auf ausschließlich lokalen Parametern beruhen und die zu denselben Resultaten führen wie die Quantenmechanik (siehe hier und hier). Ich denke, dass schon allein die Einfachheit dieser Formeln ein Indiz dafür ist, dass die Art der Verschränkung im experimentellen Setup und somit auch in der Statistik der daraus resultierenden Messergebnisse enthalten ist. Auf die Darstellung des Ablaufs der zugehörigen physikalischen Prozesse habe ich jedoch verzichtet, weil mehrere Zusatzannahmen sie in meinen Augen unattraktiv machen. Ich glaube, dass der Weg zu einem detaillierten Verständnis, was in EPR-Szenarien wirklich vor sich geht, nur mit experimenteller Unterstützung möglich sein wird.

Entscheidend ist jedoch, dass es gelungen ist, Bells Beweis zu widerlegen – oder sagen wir besser: außer Kraft zu setzen. Dadurch ist es nun möglich, die Lokalität der Wirklichkeit anzunehmen, ganz so, wie es Einstein im Sinn hatte. Ich muss zugeben, dass mir diese Annahme schon immer als eine selbst­verständliche Forderung der Vernunft erschienen ist.

Mit diesem ersten, wichtigen Schritt zu einem tieferen Verständnis der Wirklichkeit ist die Angelegenheit jedoch offen­sichtlich nicht erledigt: Die Annahme, dass nicht das Teilchen, sondern die Akkumulation von Wellen das Ereignis verursacht, steht in eklatantem Widerspruch zu dem seit 1905 geltenden, von Einstein eingeführten Modell der Wechselwirkung von Licht und Materie.

Also muss als nächstes dieser Widerspruch aufgelöst werden. Das geschieht in den beiden Aufsätzen Licht­elektrischer Effekt und Compton-Effekt.

Dieser Schritt zieht weitere nach sich, und es ist tatsächlich erst dann möglich, den Weg zu beenden, wenn eine vollständige Umstellung des gesamten physikalischen Interpretations­netzes erfolgt ist. (Siehe Lokale und objektive Interpretation der Quantentheorie und Neuinter­pretation der Speziellen Rela­tivitäts­theorie.)

Das führt dann wiederum dazu, dass die begrifflichen Grundlagen der Physik erneuert werden müssen. (Siehe Grundlagen einer neuen Physik.)

Bei diesem Versuch eines Neuaufbaus bewähren sich die Vorstellungen, die schon zu Anfang – bei der Wieder­herstellung der Lokalität – zum Erfolg führten. Sie ermöglichen einsichtige geometrische Begründungen von Gravitation und Elektro­magnetismus, Atomaufbau, Anti­materie sowie etlichen weiteren physikalischen Relationen. Überdies führt die veränderte Sicht der Natur zu einer alternativen Kosmologie, in der die Konzepte Dunkle Energie und Dunkle Materie ebenfalls eine einfache Erklärung finden.

Das ist aber noch nicht alles; Von der neuen begrifflichen Basis aus gelingt schließlich auch die Integration von Materie und Geist in ein und dasselbe Bild der Wirklichkeit. (Mehr dazu in den drei Abhandlungen Willensfreiheit, Das veränderte Bild der Wirk­lichkeit und Qualia.)

Zuletzt noch ein persönliches Wort zu dieser Homepage.

Ich beziehe weit außerhalb des Mainstreams Position – in einer Entfernung, in der man ansonsten nur Narren trifft.

Im Allgemeinen lohnt es sich kaum, sich auf die Gedanken von Außen­seitern einzulassen. Es ist anstrengend, befremdlich, und die Wahr­schein­lichkeit, einem richtigen oder wenigstens interessanten Gedanken zu begegnen, ist gering.

Was gäbe es also für einen Grund, weiter zu lesen?

Nur diesen einen: In der Geschichte der Menschheit gibt es ein einzig­artiges Ereignis – jenen wunderbaren Moment, in dem zum erstenmal "eine Tür aufgeht und den blitzenden zentralen Mechanismus der Welt in all seiner Schönheit und Einfachheit sichtbar werden lässt" (John Archibald Wheeler).

Genau das geschieht hier. Der seltsame Nebel, der derzeit unseren Blick auf die Wirklichkeit trübt, lichtet sich, die erkenntnis­theoretische Verwirrung löst sich auf, und der fundamentale Prozess, der fort­während die Wirklichkeit hervorbringt, wird erkennbar.