Is the World Nonlocal?
At present, 96 percent of what the universe contains is completely unknown. For 22 percent – the so-called dark matter – there are some candidates in various speculative concepts beyond the standard model of particle physics, however as regards the remaining 74 percent – the so-called dark energy – we are utterly ignorant.
So maybe now, in view of such a vast terra incognita, is the right time to ask anew the most general and most fundamental of all questions:
What is the world made of?
Currently, this question can only be answered with a clear: "We do not know". That alone would already be unsettling, however our situation is indeed much worse, almost hopeless: It even seems as if we had to admit that it is completely impossible for us to know what the world ultimately consists of and what is going on at the bottom of things. Paradigmatic scenarios from quantum mechanics – such as the "double-slit experiment" – demonstrate the futility of any attempt to form an idea of what is actually happening there.
Is this failure final? Are our concepts in fact so completely unsuitable for understanding reality?
The answer is no!
Within this brief introduction, however, it is not possible to describe how the understanding of reality can be restored, but at least I shall make a start by outlining how the seemingly irrefutable proof of quantum mechanical nonlocality – the so-called Bell's Inequality – is overridden by a simple change of perspective.
In the historical development of the interpretation of quantum theory, it was this proof that put an end to all attempts to conceive an idea of what quantum objects actually are and what in fact occurs in quantum mechanical measurement processes. So if one doesn't accept this ontological blindness but still aims to comprehend reality, the first step must be to refute this very proof.
What is "nonlocality"? This can be illustrated using the Einstein-Podolsky-Rosen Paradox. To understand the paradox, a few facts will suffice:
(1)![]() Generally, the quantum mechanical description of an object determines for some attributes not a definite value but only the probability distribution of possible measurement values.
Generally, the quantum mechanical description of an object determines for some attributes not a definite value but only the probability distribution of possible measurement values.
(2)![]() This applies also to the case of two spatially separated objects which interacted in the past or which originate from the decay of an object.
This applies also to the case of two spatially separated objects which interacted in the past or which originate from the decay of an object.
(3)![]() Between the outcomes of certain measurements on these two objects there will then be a connection that is called "entanglement". E.g. in the case of two identical particles A and B which come from the decay of an object at rest and depart into opposite directions, the two momentums are interconnected in the same way as in classical physics, which means they are identical except for the sign. Another example: If a spin 0 system decays into two photons, then the measured polarization directions of the photons are rectangular to each other.
Between the outcomes of certain measurements on these two objects there will then be a connection that is called "entanglement". E.g. in the case of two identical particles A and B which come from the decay of an object at rest and depart into opposite directions, the two momentums are interconnected in the same way as in classical physics, which means they are identical except for the sign. Another example: If a spin 0 system decays into two photons, then the measured polarization directions of the photons are rectangular to each other.
That's all there is to it! What is paradoxical about it? This is quickly explained, too:
Let us assume as yet no measurement has been performed. Thus only the probability distribution of the measurement values is known. But if now the momentum of particle A is measured, then, because of (3), at the same moment also the momentum of B is known, and the same applies to the case of the photon polarizations.
Now one can argue with Einstein, Podolsky and Rosen in the following way:
B is at an arbitrarily great distance from A. Therefore, the measurement on A cannot have influenced B. Thus we can state: if B has a definite momentum after the measurement on A, then it must have had this momentum also already before the measurement on A – otherwise the measurement on A would have caused a change of the state of B. However, since the quantum mechanical description does not contain this momentum, it must be considered incomplete. (In this case, the momentum would be a so-called hidden parameter.)
That sounds like a reasonable argument! Indeed the alternative would be to assume a nonlocal connection between the two measurements, that is a connection which requires either a faster-than-light transmission or which exists without any mediating process at all and must simply be accepted as such.
However, as John Bell showed almost 30 years later (John Stewart Bell, On the Einstein Podolsky Rosen Paradox, Physics, 1, 195-200, 1964), this apparently so reasonable EPR assumption – that the measurement result on B is determined already before the measurement on A, because it simply corresponds to an attribute of B – has a consequence that Einstein, Podolsky and Rosen had not expected.
Bell proved the following:
Provided that the EPR assumption is correct, there are experiments in which the measurement results deviate significantly from the predictions of quantum mechanics. Such experiments were carried out. The decision was clear: the predictions of quantum mechanics were confirmed, the EPR assumption was thus refuted. This means: Before the measurement on A, B has no definite momentum, afterwards it does have one. The measurement on A actually changed the state of B!
EPR had intended to argue for a local reality, i.e. for a reality in which an object cannot act on another, spatially distant object other than through a physical process. However Bell's intervention seems to have proven that there are also connections of a completely different kind: connections which are either mediated faster than light or which even exist without any mediation. Einstein called that "Spooky action at a distance".
John Bell formulated his proof as general as possible. In this generalized form of the proof, it is not necessary that "object properties" specify the measurement result in advance, instead it could be any parameters. In his own words: "Let this more complete specification be effected by means of parameters λ. It is a matter of indifference in the following whether λ denotes a single variable or a set, or even a set of functions, and whether the variables are discrete or continuous." (John Bell, lc, p. 196).
This generalization expands the scope of the proof. And since, apart from the assumption of the parameters λ (and of course logic and mathematics), no further assumptions are necessary for the proof, the following conclusion seems unavoidable:
Any reality that obeys the laws of quantum mechanics is non-local.
So much for the situation. In physics, the question of locality or non-locality is considered to be settled, and entanglement is a much-noticed, active area of research.
For us, however, the presentation of the usual point of view is only intended to serve as a preparation for our actual task, the answer to the question:
Why does Bell's proof not apply to our reality?
To answer this question, I will draw on the model which I developed in the analysis of the double-slit experiment; It allows a realistic and local interpretation of the experiment, which can be transferred to the EPR scenario. So I will briefly outline what, according to my interpretation, actually happens in this experiment. (For a more extensive explanation see The Double-Slit Experiment - What Really Happens.)
First, an electron detaches from an orbital (an electron shell). The following image shows the pictures of some orbitals:
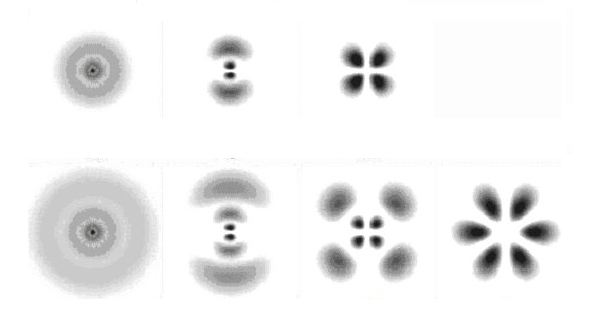
As can be seen,"electron shells" correspond to oscillation states of a sphere, in other words: they ARE three-dimensional standing waves. If an "electron" is released from such a standing wave, then (so to speak) part of the standing wave becomes a running wave. The remaining standing wave has one nodal surface less. The electron – the running electron wave – then crosses the double slit. After the double slit, it diverges and interferes with itself. Finally it arrives at the detector plate, and this means: wherever its amplitude is not zero, it hits an orbital – a standing electron wave. Since it must be assumed that several of these standing waves are already close to the limit above which they "jump" to the next higher state – the state with one more nodal surface – the running wave will somewhere trigger such a jump with a certain probability, in other words: at this point an "electron" appears.
The rest of the running electron wave does not disappear as in the standard interpretation, but adds up to the other standing electron waves, whereby the probability increases everywhere that the next incoming electron wave or any subsequent one will cause a jump.
In order to establish the connection with the EPR scenario, let us consider the "object" we have just described, i.e. the "electron".
Let us first ask: Does this electron have a definite position?
To the electron that we finally observed on the detector plate, undoubtedly a relatively precisely defined position can be ascribed. But as we know, this electron is not that electron that was underway before. The newly created oscillation area in the standing electron wave, which in our view is the observed electron, contains only a tiny fraction of the entire running wave that the electron was before. The rest of the running wave is now distributed over all other standing waves.
So it is very clear: The electron that we observe did not have a definite position before the measurement, because before the measurement this "electron" did not even exist!
From this follows that the model concept which Einstein, Podolsky and Rosen's argument is based on, is completely inappropriate. They thought of an object that always remains identical with itself and moves on a path so that it has a definite position at all times. It is therefore evident that the EPR assumption (that the object attribute already exists before the measurement) is wrong.
What about the above-mentioned generalization in Bell's proof, in which the measured value is not determined by an object attribute but by arbitrary parameters λ?
This question leads us directly to the core of our refutation of Bell's proof. As follows:
As can be seen from the above quotation, Bell assumes the existence of parameters λ which ensure the "more complete" specification of the measured values for any measurements on the selected objects. ("More complete" because in quantum mechanics they do not exist or are "uncertain"). The existence of the parameters λ ensures that we can predict the exact measurement result in any case.
At the center of Bell's proof is an inequality that contains both the results of measurements that can actually be carried out, and the results of further, hypothetical measurements on the same objects. ("Hypothetical" because the measurement objects are of course not available again.)
This means:
The knowledge what results further measurements on the same objects would lead to is necessary for establishing the proof. Without this knowledge, there is no Bell proof.
Let us now return to our model. Is it possible here to predict the results of further measurements on the same objects?
Suppose we have created an electron. It crosses the double slit, diverges and interferes with itself. A tiny part of the electron induces a standing electron wave on the surface of the detector plate to jump to the next higher state. A black point can be seen there, indicating that an electron has appeared. We have measured the position of this electron.
Can we now carry out another measurement with the electron that we have generated just before? (It is not the one whose position we have just measured!) Of course not – this "electron" no longer exists because it is now distributed over all orbitals – but we can generate an electron that is almost identical to the one previously generated, and that is sufficient for our train of thought: We cannot carry out another measurement on the same object, but we can repeat the measurement process.
Now to the crucial question: what will happen when this electron reaches the detector plate? At which position on the detector plate will an electron appear?
The answer is: we cannot know. The position of the next jump – i.e. the next appearance of an electron – depends not only on the amplitude distribution of the wave that hits the plate, but also on how far the standing electron waves on the plate are away from the jump to the next state, and that is constantly changing. There is no measuring process in which, for all electron waves, the distances from this jump limit are equal to the distances that they have in any other measuring process. ("Distance" is defined here by how large the amplitude square of the impinging electron wave must be at least in order to trigger a jump to the next higher state).
In other words:
It is impossible to predict the exact position of the appearence of any electron.
What we have just shown for a position measurement in the double slit experiment also applies to the measurements of the attributes of entangled objects in EPR scenarios. Let us consider, for example, the case that has been best investigated experimentally: polarization measurements on entangled photons.
First the usual description: Photons are generated in pairs. On their way they reach polarizers which they cross with a certain probability. If they get through, they hit a detector and a photon is registered. If they don't get through, no photon will appear.
Now to the explanation of what is really happening. It follows the same principle as in the double slit scenario: Photons ARE light waves. When passing through the polarizers, their amplitudes decrease by the factor cos α (α is the angle between the direction of oscillation of the wave and the plane of the polarizer). When a light wave reaches the detector, it possibly causes a transition of a standing electron wave to a higher state – then a "photon" is detected. If there is no transition, the light wave still adds up to one or more electron waves and thereby increases the probability of a transition when the next light wave hits or one that follows later. This means: every later measurement is affected by every earlier one. Even if we were able to measure the same photon pairs again, it would not be possible to predict the measurement results.
Bell's proof would only be feasible if the test series consisted of measurements that are independent of one another. The following should therefore apply: as soon as a measurement result is available, the respective measurement process is completely finished and does not affect the further measurement processes. (If the order was altered, the measurement results would remain unchanged.)
This is obviously not the case in our model: As just explained, every light wave that reaches the detector changes some of the standing electron waves (orbitals) – even if this change does not lead to a jump to the next higher state. So, here, there are no test series that consist of individual events that are independent of each other, but only test series in which any subsequent measurement is influenced by any preceding one. Thus, the starting conditions of any individual measurement change in an unpredictable way, and this means:
There are no parameters λ, from which the measurement results follow. Bell's proof cannot be derived.
In order to avoid any ambiguity here, I would like to emphasize the essential point again. Of course there are parameters in my model that completely determine each measurement result, but since these parameters also include how far the standing electron waves are away from the limit above which they jump to the next higher state, when an incoming light wave hits, these parameters do not meet the condition that must be fulfilled for Bell's parameters λ: Bell's parameters make the measurement on a certain object repeatable, they ensure that the results of further measurements on the same object are known. However, the "distances" from the jump limit change each time a new measurement is carried out (presumably they are also subject to constant fluctuations regardless of any measurement), and therefore also the result of the measurement on a certain object changes with each repetition. Thus there is no "more specific" prediction of any measurement – it sticks to the quantum mechanical probability.
We have thus achieved our goal. For this it wasn't even necessary to go into the proof itself – for our reasoning, the analysis of the measurement process was perfectly sufficient.
What is missing here, however, is a detailed description of what really happens in EPR test series. If the measured value cannot be predicted before the measurement – what actually ensures the connection between the measured values of the entangled objects?
In The Concept of Reality, I have given a formula for the event probabilities that is based on exclusively local parameters and that leads to the same results as quantum mechanics (see here). I think that the simplicity of this formula is already an indication that the specific type of entanglement is somehow contained in the experimental setup and thus also in the statistics of the resulting measurements. However, I refrained from describing the associated physical processes because, in my eyes, several additional assumptions make them unattractive. I believe that the path to a detailed understanding of what is really going on in EPR scenarios will only be possible with experimental support.
The decisive factor, however, is that we succeeded in refuting Bell's proof – or, better said, in overruling it. As a result, it is now possible to claim the locality of reality, just as Einstein had in mind. I have to admit that this assumption has always seemed to me to be an obvious demand of reason.
However, with this first important step towards a deeper understanding of reality, the matter is obviously not done: The assumption that not the particle but the accumulation of waves causes the event is in blatant contradiction with the model of the interaction between light and matter, which exists since 1905 and was introduced by Einstein.
Thus, next this contradiction has to be resolved. This is done in the two papers Photoelectric Effect and Compton Effect.
This step entails further ones, and it's actually impossible to end the way before a full conversion of the entire physical interpretation network is carried out. (See Local and objective Interpretation of Quantum Theory – among other things, here is explained what actually happens in the double slit experiment (starting on page 23) –, and Reinterpretation of Special Relativity.)
This in turn has the consequence that the conceptual foundations of physics must be rebuilt. (See Basics of a New Concept of Physics.)
In this attempt at rebuilding physics, the ideas that already at the beginning – in the restoration of locality – have led to success, again prove successful: They permit understandable geometric substantiations of gravitation, electromagnetism, atomic structure and antimatter as well as of several other physical relations. Moreover, the modified view of nature leads to an alternative cosmology, in which the concepts "dark energy" and "dark matter" likewise find simple explanations.
That's not all, though: Starting from the new conceptual basis, finally matter and mind can be integrated into one and the same picture of reality. (More on that in the three treatises Free Will, The Modified Picture of Reality and Qualia.)
At last, a personal word about this website.
I take a position far outside the mainstream – at a distance, where in general only fools reside.
In general, it is hardly worthwhile to engage with the ideas of outsiders. It's exhausting, disconcerting, and the chance to meet a correct or at least an interesting thought is low.
So, what reason would be there to read further?
Only this one: In the history of mankind, there is a unique event – that wonderful moment when, for the first time, "a door opens and exposes the glittering central mechanism of the world in its beauty and simplicity" (John Archibald Wheeler).
This is what happens here. The strange fog that currently obscures our view on reality clears, the epistemological confusion dissolves, and the fundamental process that permanently generates reality becomes apparent.