Heinz Heinzmann

Der Weg zur Auflösung des EPR-Paradoxons

Der Kürze halber habe ich in den auf meiner Seite Physik aufgelisteten Arbeiten zum EPR-Szenario nur die Lösung selbst notiert, aber nicht den Gedankengang und den formalen Weg zu dieser Lösung. Deshalb nun eine kurze Beschreibung dieses Wegs.

Die QM-Formel für den Zustand verschränkter Photonen, die dem Zerfall eines Spin-0-Systems entstammen, lautet
(δ Winkel zwischen den Polarisatoren)

Somit ist die Wahrscheinlichkeit des gleichzeitigen Auftretens von Photonen in beiden Detektoren

Eine objektive, lokale Interpretation von (0) erfordert, (0) statistisch zu interpretieren, d.h. es als Ausdruck für den Mittelwert einer Zufallsfolge aufzufassen, wobei aber die cos- und sin- Terme nicht als Polarisationszustände von Photonen verstanden werden dürfen – sonst würde sich eine Ensemble-Interpretation ergeben – sondern als Amplituden von Lichtwellen, die die Polarisatoren durchquert bzw. nicht durchquert haben. Wenn wir annehmen, dass zwischen der Polarisation der Wellen links und rechts immer ein Unterschied von 90° besteht, dann ist cosα die links, cos(α+90-δ) = –sin(α-δ) die rechts durchgegangene Wellenamplitude, und sinα die links, sin(α+90-δ) = cos(α-δ) die rechts durch den Polarisator aufgehaltene Wellenamplitude. (Da die Quantenmechanik nichts über die Polarisation dieser Wellen sagt – sie kommen dort ja gar nicht vor – können die Wellen mit verschiedenen Polarisationsrichtungen auch durchaus einem einzigen Zerfallsprozess entstammen.)

Statistisch interpretiert, wird (0) zu

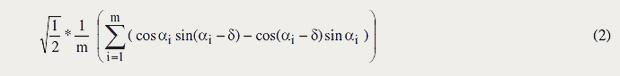
Zunächst ist klar, dass es möglich sein muss, die Wahrscheinlichkeiten nur durch die Amplituden der durchgegangenen Wellen auszudrücken: diese sind es ja, die das Ereignis verursachen. Wir müssen also den zweiten Term eliminieren.