Heinz Heinzmann

The Way to the Solution of the EPR-Paradox

For the sake of conciseness, in the papers on EPR listed on my site Physics only the solution itself is noted but not the train of thought and the formal way to the solution. Therefore I shall give here a short outline of this way.

The QM formula for the state of two entangled photons, which originate from the decay of a spin-0 system, is
(δ is the angle between the two polarizers)

Thus the probability of the simultaneous appearance of photons in both detectors is

An objective and local interpretation of (0) requires to take (0) as a statistical formula, i.e. to interpret it as mean value of a random sequence where, however, the cosine and sine terms cannot be seen as polarization states of photons – this would lead to an ensemble interpretation – but as amplitudes of light waves that have passed or have not passed the polarizers. If we assume that the angle between the polarization directions of the waves to the left and those to the right is always 90°, then cosα is the amplitude of a wave that has passed the left polarizer, cos(α+90-δ) = –sin(α-δ) the according amplitude on the right side, and sinα is the amplitude of a wave to the left that has not passed, sin(α+90-δ) = cos(α-δ) the according amplitude to the right. (Since Quantum Mechanics does not say anything about the polarization of these waves – they do not even exist in QM – the waves with different polarization directions can originate also from one single decay.)

Interpreted statistically, (0) becomes

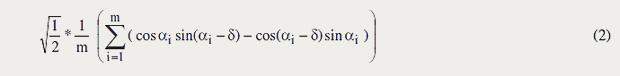
At first it is evident that it must be possible to express the event probabilities only by the amplitudes of the waves that have passed the polarizers: indeed it is these very amplitudes that cause the events. Thus we have to eliminate the second term.